Helium 4 And Quantum Effects
Unlike every other element on the periodic table, helium has the distinctive property
that, under standard pressures, it does not crystalise into a solid form as the temperature
is decreased toward absolute zero. From the phase diagram of Helium 4 below, it is clear that helium
does have a solid phase so why is it only accessible under the most extremes of pressure?
The answer requires an understanding of the quantum nature of the solid crystal phase. In particular, it is essential to understand the De Broglie length scale and the zero point energy of helium.
de Broglie Length Scale
If helium were to crystallise into a solid, each helium atom could be modelled as being connected by springs
to its nearest neighbours. As it has six degrees of freedom (three from the kinetic energy term and three from the potential), its mean energy is \(E = 3k_BT\) via the Equipartition Theorem. As such it has a momentum \(E = 3k_BT = \frac{p^2}{2m} \Rightarrow p=(6mk_BT)^{\frac{1}{2}}\).
The thermal de Broglie wavelength sets the scale for quantum effects and if it is of comparable size to other length scales in the system, quantum effects will dominate. It is given by
\(\lambda_{dB}(T) = \frac{h}{p} = \frac{h}{(6mk_BT)^{\frac{1}{2}}}\)
Figure 2 below shows the interatomic potential of helium. The shallow depth of the well results in weak binding between
helium atoms. As such, liquid helium is only possible at around \(T \approx 4K\). This is a good estimate for the \(T\) in the de Broglie wavelength expression. At this temperature, the de Broglie wavelength is \(\lambda_{dB} \approx 0.4nm \) but the minimum in the potential occurs at \(r = 0.3nm\). Quantum effects are expected to dominate and one such effect is the zero point energy.

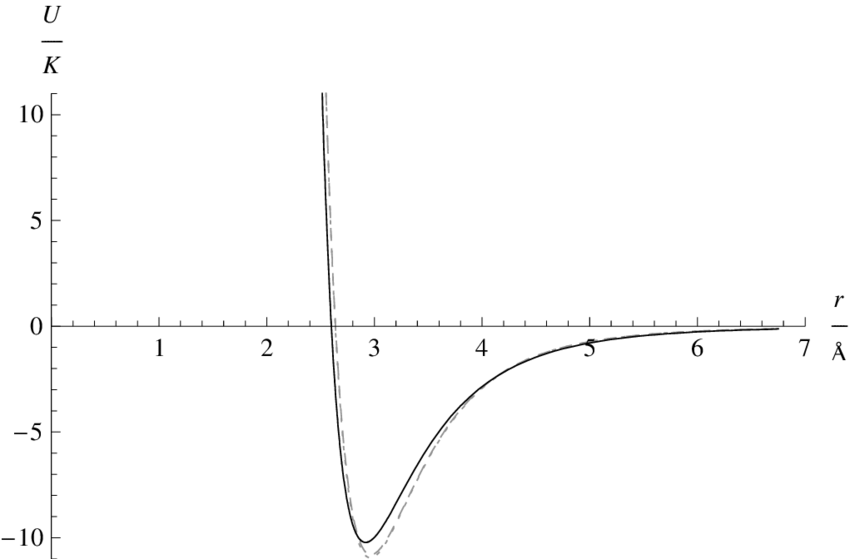
Zero Point Energy
The zero point energy is the energy attributed to a harmonic oscillator that is in its ground state. When the temperature is low enough, a atom will not have attain the thermal energy to be promoted to
an excited state and so must reside in its ground state. The interesting physics arises from the fact that the zero point energy of this state is not zero! Instead, the zero point energy may be great enough to allow the atom to jump out of a potential well such as in Figure 2, preventing a solid from forming.
The zero point energy is given by by \(E_0 = \hbar\omega = \hbar\sqrt{\frac{k}{m}}\). \(\omega\) is the natural frequency of the oscillator, \(k\) is the mechanical spring constant of the "atoms joined by springs" model and \(m\) is the mass of the atom. \(k\) can be calculated from the curvature of the interatomic potential at the minimum. The low mass and strong curvature of the potential results in a high zero point energy: \(E_0 \approx 7meV\). This is equivalent to being in thermal equillibrium of a temperature bath at 70\(K\) and is more than enough to stop crystallisation.