Properties of Superfluids

The phase diagram on the helium page reveals the existence of two liquid phases of matter- the normal fluid and the superfluid phases. These two phases are denoted He I and He II respectively. He I behaves as a regular fluid; it has viscosity, it carries heat and it stays in whatever container it is kept in. For He II, it is often the case that none of these are true!

He II is cleary very different from everyday fluids and to really make this point concrete, it is worth examining some of its extraordinary properties.

The He I - He II Transition

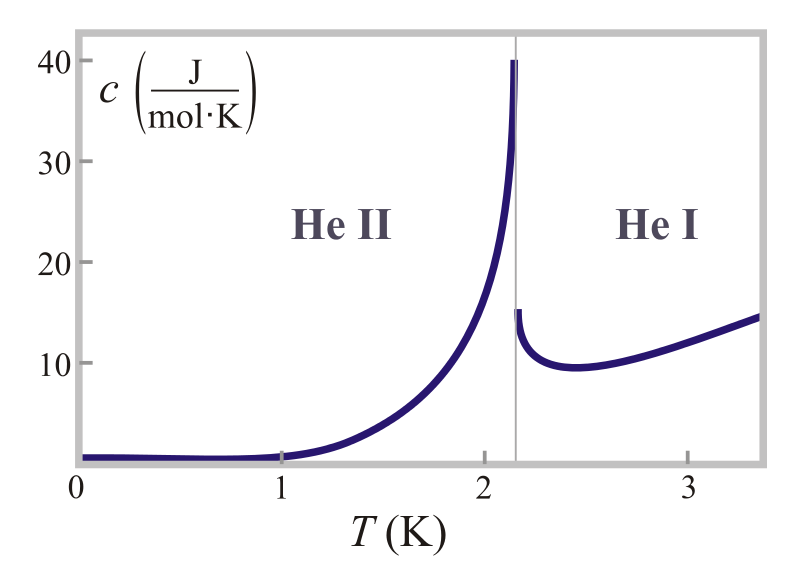
As He I behaves as a regular fluid, the interesting physics and unusual phenomena are contained in the He II phase. As the temperature is lowered under standard pressures, He I undergoes a phase transition to He II at \(T = 2.17K\). This is a definite thermodynamic phase transition as there is a discontinuity in the derivative of the heat capacity, as seen on Figure 1.

Due to the likeness of the heat capacity graph to a \(\lambda\), the transition temperature is called the \(\lambda\) point. The change in the temperature dependence of the heat capacity is just one property that changes between the superfluid and helium phases.

A good demonstration of the transition is presented in the BBC's Horizon programme.

Fig 1: The Heat Capacity Lambda Point

Experiments With He II

The superfluid He II phase of helium was confirmed by Kapitsa in 1938 and since then a whole host of experiments have been conducted using it. These include:

  • Superflow: In the 1930s, He II was shown to flow through a capilliary with no resistance. It was said to exhibit a superflow meaning He II flows with zero viscosity; a completely novel property in fluids.
  • Rotating Disks : A disk suspended in fluid from a wire can oscillate due to the torsional stiffness of the wire. Submerge the disk in a viscous fluid and the fluid is dragged along with the rotating disk, reducing the frequency like a damped harmonic oscillator. This reduction in frequency also occurs when the disk is submerged in He II implying He II has viscosity. An apparent contradiction!
  • Fountain Effect : If two containers of superfluid He II at different temperatures are connected by an extremely narrow capilliary, the two containers remain at different temperatures and a mantain a constant pressure difference. The two containers never equillibriate and fluid can continue to flow.
  • Spontaneous Emptying : He II kept within a container that is open to an atmosphere of a higher temperature can spontaneously climb out the side of the container and empty.

    • A few of these can be seen in the famous Alfred Leitner lecture embedded.

Macroscopic Wave Functions

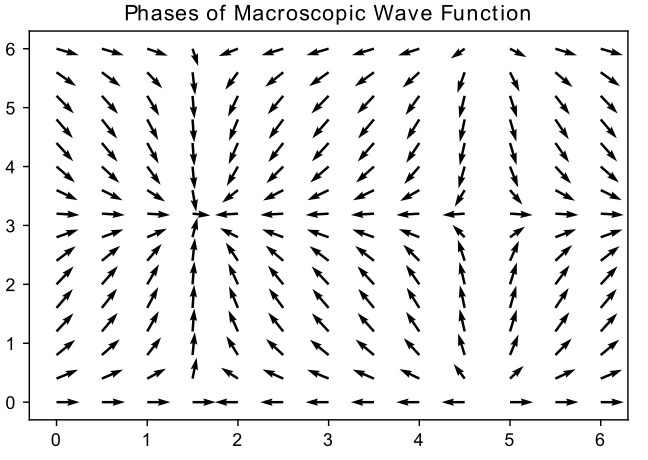
Some of these effects can be described by the idea of a macroscopic wavefunction. This is the idea that, once the temperature has been lowered to below the \(\lambda\) point, the entire fluid can be described as a single state known as the condensate. This explains why the fluid appears completely still as it transitions to the He II phase - it cannot interact with itself.
Mathematically, this single state can be represented as \(\Psi(\mathbf{r}) = \sqrt{n_0(\mathbf{r})}e^{i\theta(\mathbf{r})}\) where \(n_0\) is the number density of particles in the condensate state. This is sensible as it means the probability ( \(|\Psi|^2\) ) of finding a particle at \mathbf{r} is proportional to \(n_0(\mathbf{r})\).
The fact that the superfluid is a single state explains the fountain effect. A single, macroscopic state has no entropy and therefore carries no heat. This prevents the two containers from coming into equillibrium.

Fig 2: The Fountain Effect
Fig 3: Ratio of fluid component density

Two Fluid Hydrodynamics

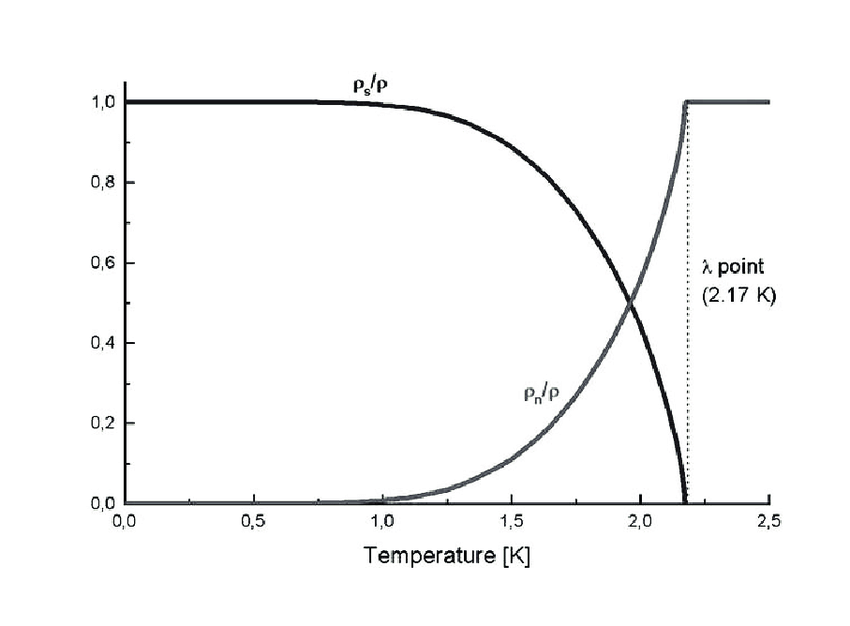
The contrasting results of the experiments that attempted to determine the viscosity of He II suggested that He II sometimes had viscosity and sometimes did not. It seems that it acts as both a normal fluid and a superfluid at the same time. This brought about the two fluid model of He II. For He II with a particle density \(n\):
\(n = n_n + n_s\)
where \(n_n\) is a normal fluid component and \(n_s\) is the superfluid component. As the temperature is changed, the ratio of the two components change (Figure 3) and for temperatures higher than the \(\lambda\) point, the superfluid component \(n_s=0\).
The superfluid component participates in superflows and carries no entropy. The two components flow with different speeds and these speeds are defined by
\(\mathbf{j_s} = n_s\mathbf{v_s}\) and \(\mathbf{j_n} = n_n\mathbf{v_s}\)

Superflow Velocity

To find the velocity of the superflow \(\mathbf{v_s}\), the probability current equation can be used. As the superfluid component can be described by a single wavefunction, the flow of the fluid can be equated to the flow of the wavefunction ie.
\(\mathbf{j_s} = \frac{\hbar}{2mi}\left(\Psi_0^*\nabla\Psi_0-\Psi_0\nabla\Psi_0^*\right)\)
Substitution of the condensate wave function gives
\(\mathbf{j_s} = \frac{h}{m}n_0\nabla\theta\)
so
\(\mathbf{v_s} = \frac{h}{m}\nabla\theta\)
So the superflow velocity depends on the phase of the condensate. In the He II phase, this phase parameter is ordered throughout the superfluid - a property known as long range order.

Fig 4: Long Range Order Of Condensate Phase