Quasiparticle Excitations
From a microscopic viewpoint, what exactly is it that distinguishes a superfluid from a normal fluid? What prevents a superfluid from experiencing viscous drag as it flows through a capilliary? The dissipation could be from two sources; excitation of the fluid to take energy away from the kinetic energy of the flow or collision of a particle with the walls. It turns out that in the superfluid model, both of these occur leading to the superfluid and normal components.
Lev Landau
Before discussing the solution to the problem on zero viscosity in superfluids, it is worth discussing the solution's creator. Lev Davidovich Landau [1908-1968] was a Soviet physicist well known for having contributed to a large collection of fields in physics. His work centred on superfluids, superconductivity, phase transitions, magnetism, quantum electrodynamics and many others.
Somewhat of a child prodigy, he attended Baku State University at the age of 14, moving to Leningrad University a year later. He graduated at the age of 19 and immediately began working on prescient physics problems.He derived the concept of Landau Levels at the age of 22 and recieved the Nobel Prize in 1962 for his theory of superfluids to be discussed on this page.
Unfortunately, he could not recieve the prize in person due to his injuries sustained in a car crash the year before. He was in a coma for months and when he awoke, he never regained his proficiency for physics.

Condition Of Superfluidity
The condition for superfluidity occurs by considering the flow of a superfluid through a capiliiary in the rest frame of the fluid and then switching the the rest frame of a the capilliary. Assume that the fluid of mass \(M\), flowing with velocity \(\mathbf{v}\), is at zero temperature so it is in its ground state. If an elementary excitation appears with momentum \(\mathbf{p}\) then
\(E = E_0 + \epsilon(\mathbf{p})\)
Moving to the frame in which the capilliary is at rest, moving at velocity \(-\mathbf{v}\), the momentum is and energy
\(\mathbf{p}' = \mathbf{p} + M\mathbf{v}\) and \(E' = E_0 + \epsilon(\mathbf{p}) + \mathbf{p} \cdot \mathbf{v} + \frac{1}{2}Mv^2\)
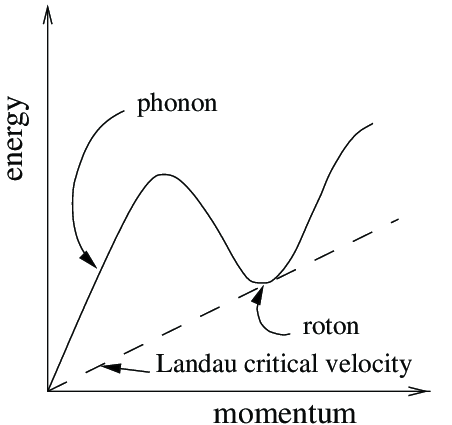
For an elementary excitation to be prohibited, the change in energy must be positive and so \(\epsilon(\mathbf{p}) + \mathbf{p} \cdot \mathbf{v} > 0\). This is Landau's criterion for superfluidity. Landau derived the form of the dispersion relation \(\epsilon{\mathbf{p}}\) and is shown in Figure 2.
Phonons and Rotons
The flow of a superfluid at non-zero temperature can be interpreted as a gas of non-interacting quasiparticles. Some of these particles are thermally excited and these can collide with the walls of the containers to produce a viscous drag effect.This is the normal component. The quasiparticles in the ground state cannot be excited by the flow of the fluid and so they constitute the superfluid.
The quasiparticles of the superfluid component are described by the dispersion relation of Figure 1. Initially, there is a linear portion for low momenta. This is similar to phonon dispersion and the physical interpretation is that the helium atoms are strongly interacting and so the whole fluid moves as a solid - just like phonons.
The quasiparticles at the minimum are called rotons with the physical interpretation being that as an atom moves forward, it's nearest neighbours must move out the way and end up behind it. In other words they rotate around the moving atom in an analogous ways to smoke rings.
At very high momenta, each particle moves effectivly independently of others and so the dispersion approaches that of the free particle.